Paradocs y morlin
Paradocs y morlin yw'r sylw nad yw'n sythweledol nad oes gan arfordir ynys hyd wedi'i ddiffinio'n dda. Mae hyn yn deillio o briodweddau arfordiroedd sy'n debyg i ffractal, h.y. y ffaith bod gan forlin ddimensiwn ffractal (sydd mewn gwirionedd yn achosi'r gysyniad o hyd i fod yn anghymwys). Arsylwodd Lewis Fry Richardson ar y ffenomen hon yn gyntaf ac ymhelaethwyd arni gan Benoit Mandelbrot.[1]
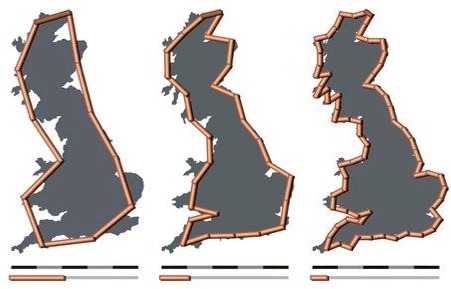
Mae hyd a fesurwyd morlin yn dibynnu ar y dull a ddefnyddir i'w fesur, a graddfa'r cyffredinoli cartograffig. Gan fod gan tiroedd nodweddion ar bob graddfa, o faint gannoedd o gilometrau i maint ffracsiynau bach milimetr ac is, nid yw'n amlwg maint pa nodwedd leiaf y dylid ei hystyried wrth fesur, ac felly does dim perimedr i'r tir sydd wedi'i ddiffinio'n dda. Mae brasamcanion amrywiol yn bodoli os byddwn yn gwneud rhagdybiaethau penodol am main lleiaf nodwedd.
Mae'r broblem yn wahanol iawn i fesur ymylon symlach eraill. Mae'n bosibl, er enghraifft, i mesur hyd bar metel ddelfrydol yn gywir trwy ddefnyddio dyfais fesur sy'n penderfynu bod y hyd yn llai na rhyw maint penodol ac yn fwy na rhyw maint arall - hynny yw, ei fesur o fewn rhyw cywirdeb penodol, a rhyw ansicrwydd penodol. Po fwyaf cywir yw'r ddyfais fesur, po fwyaf agosbydd y canlyniadau at wir hyd yr ymyl. Wrth fesur morlin, fodd bynnag, nid yw'r mesuriad agosach yn arwain at gynnydd mewn cywirdeb, ond at cynnydd mewn hyd; yn wahanol i'r bar metel, nid oes unrhyw ffordd i gael y gwerth mwyaf am hyd yr arfordir.
Mewn gofod tri dimensiwn, mae paradocs yr arfordir yn cael ei ymestyn yn rhwydd i'r cysyniad o arwynebau ffractal lle mae arwynebedd arwyneb yn amrywio, yn dibynnu ar y cydraniad mesur.
Agweddau mathemategol
golyguMae'r cysyniad sylfaenol o hyd yn gwreiddio o bellter Ewclidaidd. Mewn geometreg Ewclidaidd mae llinell syth yn cynrychioli'r pellter byrraf rhwng dau bwynt. Dim ond un hyd sydd gan y llinell hon. Ar wyneb sffêr, y hyd hwn yw'r geodesig (a elwir hefyd yn hyd cylch mawr), sy'n cael ei fesur ar hyd y gromlin arwyneb sy'n bodoli yn y blân sy'n cynnwys y ddau bwynt terfyn a chanol y sffêr. Mae hyd cromliniau sylfaenol yn fwy cymhleth, ond gellir eu cyfrif hefyd. Trwy fesur gyda phren mesur, gallwn amcangyfrif hyd cromlin trwy symio'r llinellau syth sy'n cysylltu'r pwyntiau:
Os defnyddir ychydig o linellau syth i amcangyfrif hyd cromlin, cawn amcangyfrif sy'n is na'r gwir hyd; pan ddefnyddir llinellau mwymwy fyr (ac felly mwy niferus), mae'r swm yn agosáu at wir hyd y gromlin. Gellir dod o hyd i union werth am y darn hwn trwy ddefnyddio calcwlws, y gangen o fathemateg sy'n galluogi cyfrifo pellteroedd anfeidrol o fach. Mae'r animeiddiad canlynol yn dangos sut y gell cromlin esmwyth cael hyd union yn ystyrlon:
Fodd bynnag, ni ellir mesur pob cromlin fel hyn. Mae ffractal, trwy ddiffiniad, yn gromlin y mae ei chymhlethdod yn newid yn ôl graddfa fesur. Tra bo brasamcanion cromlin esmwyth yn tueddu i werth sengl wrth i gywirdeb mesur gynyddu, nid yw'r gwerth a fesurir ar gyfer ffractal yn cydgyfeirio.
- Mae'r gromlin Sierpiński (fath o gromlin llenwi-gofod), sy'n ailadrodd yr un patrwm ond ar raddma llai ac yn llai, yn tyfu ac yn tyfu mewn hyd. Os yw'n parhau i ailadrodd mewn gofod geometre, mae ei hyd yn tueddu i anfeidredd. Ar yr un pryd, mae'r arwynebedd amgaeëdig yn cydgyfeirio i maint manwl gywir—fel, yn yr un modd, gallwn cyfrifo arwynebedd ynys yn fwy hawdd na hyd ei arfordir.
Gan fod hyd cromlin ffractal bob amser yn dargyfeirio i anfeidredd, pe bawn yn mesur morlin gyda cydraniad anfeidrol neu bron yn anfeidrol, byddai hyd pob cinc anfeidrol fyr ar yr arfordir yn symio i anfeidredd.[2] Fodd bynnag, mae'r ffigur hwn yn dibynnu ar y rhagdybiaeth y gellir isrannu gofod yn adrannau anfeidrol. Mae gwiredd y dybiaeth hon (sy'n sail i geometreg Ewclidaidd ac yn defnyddiol wrth fesur bob dydd) yn fater athronyddol, ac efallai na fydd yn adlewyrchu realiti newidiol "gofod" a "pellter" ar y lefel atomig (tua graddfa nanomedr). Er enghraifft, cynigir hyd Planck, llawer o raddau maint llai nag atom, fel yr uned fesuradwy leiaf bosibl yn y bydysawd.
Mae morlinoedd yn llai pendant yn eu hadeiladwaith na ffractalau delfrydol fel y set Mandelbrot oherwydd eu bod yn cael eu ffurfio gan amryw o ddigwyddiadau naturiol sy'n creu hap-batrymau, tra bod ffractalau delfrydol yn cael eu ffurfio trwy iteriadau ailadroddol sy'n dilyn fformiwla syml.[3]
Cyfeiriadau
golygu- ↑ Mandelbrot, Benoit (1983). The Fractal Geometry of Nature. W.H. Freeman and Co. 25–33. ISBN 978-0-7167-1186-5.
- ↑ Post & Eisen, p. 550. (see below)
- ↑ Heinz-Otto Peitgen, Hartmut Jürgens, Dietmar Saupe, Chaos and Fractals: New Frontiers of Science; Spring, 2004; p. 424.