Pyramid sgwâr

Mewn geometreg, math o byramid yw 'pyramid sgwâr, gyda'i sylfaen yn sgwâr. Os yw'r apig yn berpendicwlar uwchlaw canol y sgwâr, mae'n byramid sgwâr, ac mae ganddo gymesuredd C4v. Os yw'r holl ymylon yn gyfartal, mae'n byramid sgwâr hafalochrog a chanddo gymesuredd C_4v.

Pyramid sgwâr

Rhwyd y pyramid

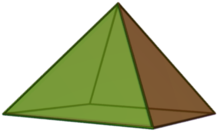
Os yw pob ochr yn hafal yna mae'n byramid sgwâr hafalochrog, sef yr hyn a elwir hefyd yn "solid Johnson J_1".

Mae gan y pyramid sgwâr arosgo (oblique), gyda hyd y gwaelod yn l a hyd ei berpendiciwlar yn h gyfaint o:

$V={\frac {1}{3}}l^{2}h$.

Y pyramid sgwâr union

Mewn pyramid sgwâr union, mae pob ymyl ochrol (lateral edges) yr un hyd, ac mae pob ochr (ar wahân i'r gwaeld) yn driongl hafalochrog cyfath.

Mae gan byramid sgwâr union gyda hyd ei waelod yn 1 a'i uchder yn h arwynebedd a chyfaint fel a ganlyn:

$A=l^{2}+l{\sqrt {l^{2}+(2h)^{2}}}$

$V={\frac {1}{3}}l^{2}h$.

Mae hyd pob ymyl ochrol yn:

${\sqrt {h^{2}+{{l^{2}} \over {2}}}}$,

ac uchder y goledd yn:

${\sqrt {h^{2}+{{l^{2}} \over {4}}}}$.

Mae'r onglau deuhedrol:

rhwng y gwaelod ac un o'r ochrau: $\arctan \left({{2\,h} \over {l}}\right)$;

rhwng dwy ochr: $\arccos \left({{-l^{2}} \over {l^{2}+4\,h^{2}}}\right)$.

Polyhedra perthynol

Pyramidiau rheolaidd
Digonal	Trionglog	Sgwâr	Pentagonal	Hecsagonal	Heptagonal	Wythonglog	Enneagonal...
Afreolaidd	Rheolaidd	Hafalochrog		Isosceles

Gellir ystyried yr Octahedron rheolaidd yn sgwâr deubyramid, h.y. dau sgwâr Johnson, gyda'u gwaelodion wedi'u cysylltu wyneb-ar-wyneb.	Gellir creu tetracis hecsahedron allan o giwb, gan roi pyramidiau sgwar, bychan ar bob ochr.	Ffrwstwm sgwâr: pyramid sgwâr gyda'r apig wedi'i flaendorri.

Ceir hefyd

• pyramid union - right pyramid
• pyramid sgwâr union - right square pyramid
• pyramid gwrthdro - inverted pyramid