Wicipedia

Seiffr Caesar

Mewn cryptograffeg, mae seiffr Caesar, a elwir hefyd y seiffr sifft, cod Caesar neu sifft Caesar, yn un o'r technegau amgryptio symlaf a mwyaf adnabyddus. Mae'n fath o seiffr amnewid lle caiff pob llythyren yn y destun-plaen ei ddisodli gan ryw lythyren unigryw arall, nifer sefydlog o safleoedd i lawr yr wyddor. Er enghraifft, gyda sifft o dri i'r chwith, bydd D cael ei ddisodli gan A, bydd E yn cael ei ddisodli gan B, ac yn y blaen. Enwir y dull ar ôl Julius Caesar, a ddefnyddiodd y seiffr hwn yn ei ohebiaeth breifat.[1]

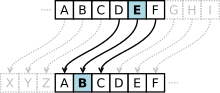
Mae seiffr Caesar yn disodli pob llythyren y destun-plaen gydag un gwahanol sydd nifer sefydlog o leoedd i lawr yr wyddor. Mae'r seiffr a ddangosir yma yn defnyddio shifft tri i'r chwith, fel bod (er enghraifft) pob llythyren E y destun-plaen yn dod yn B yn y destun-seiffr.

Mae'r cam amgryptio a gyflawnir gan y seiffr Caesar yn aml yn cael ei defnyddio fel rhan o seiffrau mwy cymhleth, fel y seiffr Vigenère, ac mae'n dal i gael ei gymhwyso'n yn system ROT13 modern. Erbyn heddiw mae'n hawdd torri seiffr Caesar, ac felly'n anymarferol oherwydd nid yw'n cynnig unrhyw ddiogelwch cyfathrebu rhagor.

Enghraifft

golygu

Gellir cynrychioli'r trawsnewidiad trwy alinio dwy wyddor; yr wyddor blaen a'r wyddor seiffr. Y wyddor seiffr yw'r wyddor blaen wedi'i sifftio i'r chwith neu'r dde gan ryw nifer o safleoedd. Er enghraifft, dyma seiffr Caesar sy'n defnyddio cylchdro dde o pum lle. Y paramedr sifft hwn yw allwedd y seiffr: 

Plaen:  A  B  C  Ch D  Dd E  F  Ff G  Ng H  I  J  L  Ll M  N  O  P  Ph R  Rh S  T  Th U  W  Y
Seiffr: Dd E  F  Ff G  Ng H  I  J  L  Ll M  N  O  P  Ph R  Rh S  T  Th U  W  Y  A  B  C  Ch D

Wrth amgryptio, mae angen edrych i fyny pob llythyren o'r neges yn y destun-blaen, ac yn ysgrifennu'r llythyren gyfatebol yn y destun-seiffr. 

Testun-plaen:  MAE HEN WLAD FY NHADAU YN ANNWYL I MI
Testun-seiffr: RDdH MHRh ChPDdG ID RhMDdGDdC DRh DdRhRhChDP N RN

Gallwn dad-seiffro'r neges trwy wneud y proses i'r cyfeiriad arall, gyda sifft o bump i'r chwith.

Gellir cynrychioli'r amgryptio hefyd gan ddefnyddio rhifyddeg fodiwlaidd (rhifyddeg cloc) trwy drawsnewid y llythrennau yn rhifau yn gyntaf, yn ôl y cynllun, A → 0, B → 1,. . ., Y → 28.[2] Gellir disgrifio amgryptio llythyren x gan shifft n yn fathemategol fel,[3]

 

Perfformir dadgryptio yn yr un modd,

 

(Mae yna ddiffiniadau gwahanol ar gyfer y gweithrediad modulo. Yn yr uchod, mae'r canlyniad yn yr amrediad 0 i 28; h.y., os nad yw x + n neu x − n o fewn yr amrediad 0 i 25, mae'n rhaid i ni dynnu neu ychwanegu 29.)

Gan fod yr amnewidiad yn aros yr un peth trwy gydol y neges, caiff y seiffr Caesar ei ddosbarthu fel math o amnewidiad monoalffabetig, yn hytrach nag amnewid polyalffabetig.

Hanes

golygu
 
Enwir y seiffr Caesar ar ôl Julius Caesar, a ddefnyddiodd y dull.

Enwir y seiffr Caesar ar ôl Julius Caesar, a'i defnyddiodd, yn ôl Suetonius, gan ddefnyddio sifft o dri amddiffyn negeseuon o arwyddocâd milwrol. Er mai Caesar oedd y cyntaf a gofnodwyd ei defnydd, roedd seiffrau amnewid eraill yn hysbys yn gynharach.[4][5]

Dydyn ni ddim yn gwybod pa mor effeithiol oedd seiffr Caesar ar y pryd, ond mae'n debygol ei fod wedi bod yn weddol ddiogel, yn bennaf oherwydd byddai'r mwyafrif o elynion Caesar wedi bod yn anllythrennog, a byddai eraill wedi tybio bod y negeseuon wedi'u hysgrifennu mewn iaith dramor anhysbys.[6] Nid oes unrhyw gofnod ar y pryd o unrhyw dechnegau ar gyfer datrys seiffrau amnewid syml. Mae'r cofnodion cynharaf sydd wedi goroesi o dadseiffro seiffrau amnewid yn dyddio i waith Al-Kindi o'r 9fed ganrif yn y byd Arabaidd. Darganfuwyd dadansoddiad amledd.[7]

Yn y 19eg ganrif, byddai'r adran hysbysebion personol mewn papurau newydd weithiau'n cael ei defnyddio i gyfnewid negeseuon wedi'u hamgryptio gan ddefnyddio seiffrau syml. Mae enghreifftiau o gariadon yn anfon cyfathrebiadau cyfrinachol wedi'u hamgryptio gan seiffr Caesar yn hysbysebion yn The Times.[8] Hyd yn oed mor ddiweddar â 1915, roedd seiffr Caesar yn cael ei ddefnyddio: roedd byddin Rwsia yn ei defnyddio yn lle seiffrau mwy cymhleth a oedd yn rhy anodd i'w milwyr deall; ond roedd yn hawdd i gryptolegwyr Almaeneg ac o Awstria i ddadgryptio'u negeseuon.[9]

Mae seiffr Vigenère yn defnyddio seiffr Caesar gyda sifft wahanol ym mhob safle'r testun; diffinnir gwerth y shifft gan ddefnyddio allweddair sy'n ailadrodd. Os yw'r allweddair cyhyd â'r neges, yn cael ei ddewis ar hap, byth yn dod yn hysbys i unrhyw un arall, ac nad yw byth yn cael ei hailddefnyddio, yna profwyd na ellir byth ei dorri. Mae'r amodau hyn mor anodd, i bob pwrpas maent byth yn cael eu cyflawni. Mae allweddeiriau sy'n fyrrach na'r neges (e.e., roedd y Cydffederaliaeth ystod Rhyfel Cartref America yn defnyddio seiffr Vigenère gyda'r allweddair "Complete Victory"), yn cyflwyno patrwm cylchol. Yn yr achosion hyn gellir ei ganfod gyda fersiwn fwy cymhleth o ddadansoddiad amledd.[10]

Ym mis Ebrill 2006, cipiwyd pennaeth y Maffia, Bernardo Provenzano, yn Sisili, rhannol oherwydd cafodd rhai o'i negeseuon, a ysgrifennwyd gan ddefnyddio amrywiad o'r seiffr Caesar, eu torri. Defnyddiodd Provenzano seiffr gyda rhifau, byddai "A" yn cael ei ysgrifennu fel "4", "B" fel "5", ac ati.[11]

Yn 2011, cafwyd Rajib Karim yn euog yn y Deyrnas Unedig o "droseddau terfysgaeth" ar ôl defnyddio'r seiffr Caesar i gyfathrebu ag actifyddion Islamaidd o Fangladesh i drafod cynlluniau i ffrwydro awyrennau British Airways neu darfu ar eu rhwydweithiau TG. Er bod gan y partïon fynediad at dechnegau amgryptio llawer gwell, fe wnaethant ddewis defnyddio eu cynllun eu hunain, a weithredwyd yn Microsoft Excel.[12]

Torri'r cipher

golygu
Sifft i'w datgryptio Testun-blaen ymgais
0 >exxegoexsrgi 
1 dwwdfndwrqfh 
2 cvvcemcvqpeg 
3 buubdlbupodf
4 attackatonce 
5 zsszbjzsnmbd 
6  yrryaiyrmlac
. . .
23  haahjrhavujl
24  gzzgiqgzutik
25 fyyfhpfytshj 

Gellir torri seiffr Caesar yn hawdd hyd yn oed mewn os oes gennych y destun-seiffr yn unig. Gellir ystyried dwy sefyllfa:

  1. mae ymosodwr yn gwybod (neu'n dyfalu) bod rhyw fath o seiffr amnewid syml wedi'i ddefnyddio, ond nid yn benodol ei fod yn gynllun Caesar;
  2. mae ymosodwr yn gwybod bod seiffr Caesar yn cael ei ddefnyddio, ond nid yw'n gwybod gwerth y sifft.

Yn yr achos cyntaf, gellir torri'r seiffr gan ddefnyddio'r un technegau ag ar gyfer seiffrau amnewid syml cyffredinol, er enghraifft dadansoddi amledd.[13] Wrth wneud hwn, mae'n debygol y bydd ymosodwr yn sylwi'n gyflym bod yna batrwm rheolaidd ac felly'n diddwytho mai seiffr Caesar a ddefnyddir.

 
Mae gan ddosraniad llythrennau mewn sampl nodweddiadol o destun Saesneg siâp unigryw a rhagweladwy. Mae seiffr Caesar yn sifftio'r y dosbarthiad hwn, ac mae'n bosibl darganfod y sifft benodol a defnyddir trwy edrych ar y graff amledd.

Yn yr ail achos, mae torri'r cynllun hyd yn oed yn fwy syml. Gan mai dim ond nifer gyfyngedig o sifftiau posib (29 yn Gymraeg, 25 yn Saesneg), gellir ceisio pob un yn ei dro mewn ymosodiad "brute-force".[14] Un ffordd o wneud hyn yw ysgrifennu darn bach o'r destun-seiffr mewn tabl o'r holl sifftiau posib.[15][16] Rhoddir enghraifft ar gyfer y destun-seiffr Saesneg "EXXEGOEXSRGI"; gallwn adnabod y destun-plaen ar unwaith fel sifft o bedwar.

Dull "brute-force" arall yw ceisio cyfateb dosraniadau amledd y llythrennau. Trwy graffio amleddau llythrennau yn y destun-seiffr, a thrwy wybod dosraniad disgwyliedig y llythrennau hynny yn iaith wreiddiol y destun-plaen, gallwn yn weddol hawdd sylwi ar werth y sifft trwy edrych ar ddadleoliad nodweddion penodol y graff. Gelwir hyn yn ddadansoddiad amledd. Er enghraifft, yn yr iaith Saesneg amleddau'r llythrennau E, T, yw'r amlaf, ac Q, Z yw'r lleiaf aml.[17] Gall cyfrifiaduron hefyd wneud hyn trwy fesur pa mor dda y mae'r dosraniad amledd gwirioneddol yn cyd-fynd â'r dosbarthiad disgwyliedig; er enghraifft gan ddefnyddio'r ystadegyn  -sgwâr.[18]

Gyda'r seiffr Caesar, nid yw amgryptio testun sawl gwaith yn darparu unrhyw ddiogelwch ychwanegol. Y rheswm am hyn yw y bydd dau amgryptiad o, dyweder, sifft A a sifft B, yn cyfateb i amgryptiad sengl gyda sifft A + B. Yn nhermau mathemategol, mae'r set o weithrediadau amgryptio o dan bob allwedd bosibl yn ffurfio grŵp o dan gyfansoddiad.[19]

Cyfeiriadau

golygu
  1. ↑ Suetonius, Vita Divi Julii 56.6
  2. ↑ Luciano, Dennis; Gordon Prichett (January 1987). "Cryptology: From Caesar Ciphers to Public-Key Cryptosystems". The College Mathematics Journal 18 (1): 2–17. doi:10.2307/2686311. JSTOR 2686311. https://archive.org/details/sim_college-mathematics-journal_1987-01_18_1/page/2.
  3. ↑ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. t. 19. ISBN 978-0-470-06064-3.
  4. ↑ "Cracking the Code". Central Intelligence Agency. Archifwyd o'r gwreiddiol ar 2020-12-26. Cyrchwyd 21 February 2017.
  5. ↑ Singh, Simon (2000). The Code Book. Anchor. tt. 289-290. ISBN 0-385-49532-3.
  6. ↑ Pieprzyk, Josef; Thomas Hardjono; Jennifer Seberry (2003). Fundamentals of Computer Security. Springer. t. 6. ISBN 3-540-43101-2.
  7. ↑ Singh, Simon (2000). The Code Book. Anchor. tt. 14–20. ISBN 0-385-49532-3.
  8. ↑ Kahn, David (1967). The Codebreakers. tt. 775–6. ISBN 978-0-684-83130-5.
  9. ↑ Kahn, David (1967). The Codebreakers. tt. 631–2. ISBN 978-0-684-83130-5.
  10. ↑ Kahn, David (1967). The Codebreakers. ISBN 978-0-684-83130-5.
  11. ↑ Leyden, John (2006-04-19). "Mafia boss undone by clumsy crypto". The Register. Cyrchwyd 2008-06-13.
  12. ↑ "BA jihadist relied on Jesus-era encryption". The Register. 2011-03-22. Cyrchwyd 2011-04-01.
  13. ↑ Beutelspacher, Albrecht (1994). Cryptology. Mathematical Association of America. tt. 9–11. ISBN 0-88385-504-6.
  14. ↑ Beutelspacher, Albrecht (1994). Cryptology. Mathematical Association of America. tt. 8–9. ISBN 0-88385-504-6.
  15. ↑ Leighton, Albert C. (April 1969). "Secret Communication among the Greeks and Romans". Technology and Culture 10 (2): 139–154. doi:10.2307/3101474. JSTOR 3101474. https://archive.org/details/sim_technology-and-culture_1969-04_10_2/page/139.
  16. ↑ Sinkov, Abraham; Paul L. Irwin (1966). Elementary Cryptanalysis: A Mathematical Approach. Mathematical Association of America. tt. 13–15. ISBN 0-88385-622-0.
  17. ↑ Singh, Simon (2000). The Code Book. Anchor. tt. 72–77. ISBN 0-385-49532-3.
  18. ↑ Savarese, Chris; Brian Hart (2002-07-15). "The Caesar Cipher". Archifwyd o'r gwreiddiol ar 2020-05-24. Cyrchwyd 2008-07-16.
  19. ↑ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. t. 31. ISBN 978-0-470-06064-3.
Wedi dod o "https://cy.wikipedia.org/w/index.php?title=Seiffr_Caesar&oldid=11844812"